微小振幅波 †
そのうちまとめます.
基礎式 †
水平・鉛直の断面2次元で,一様水深の空間を考える.
非圧縮の連続式
\[
\nabla \cdot \boldsymbol{u} = 0
\]
(\(\boldsymbol{u}\) は水粒子の速度)に対して下記のように非回転としてポテンシャル理論を適用し,
\[
\frac{\partial \phi}{\partial x} = u, \: \frac{\partial \phi}{\partial y} = v
\]
この2式からラプラスの方程式を得る.ここで \( \phi \) は速度ポテンシャル.
\[
\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2} = 0 \\
\nabla^2 \phi = 0
\]
これが渦なし流れの基礎方程式であるが,この微分方程式を満たす \( \phi \) は無数に存在する.
底面および水面での境界条件式と,速度ポテンシャル \( \phi \) や水面 \( \eta \) が周期性を持つ波であることの仮定を用いて
これらの変数の解を得る.
解の導出 †
気が向いたらちゃんと書く.
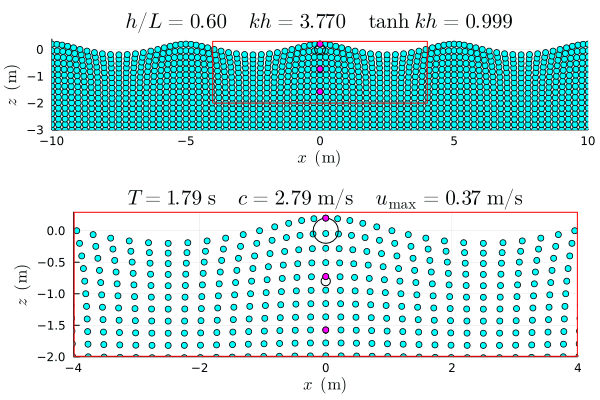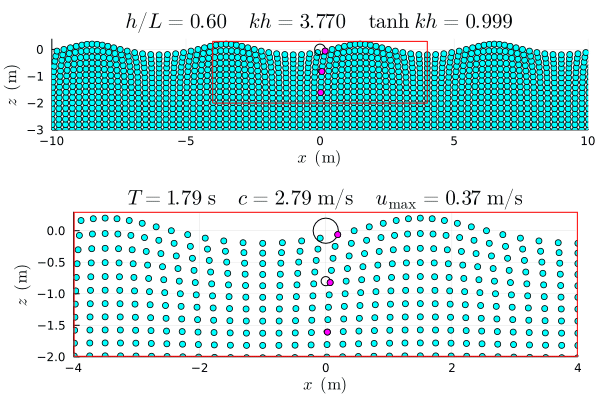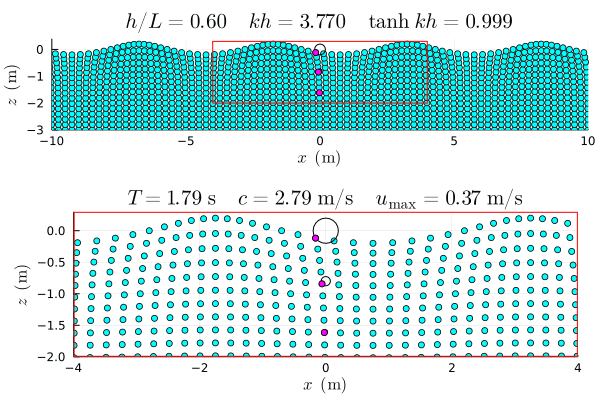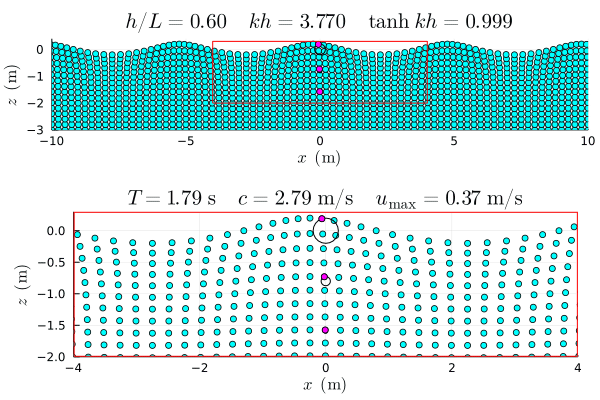
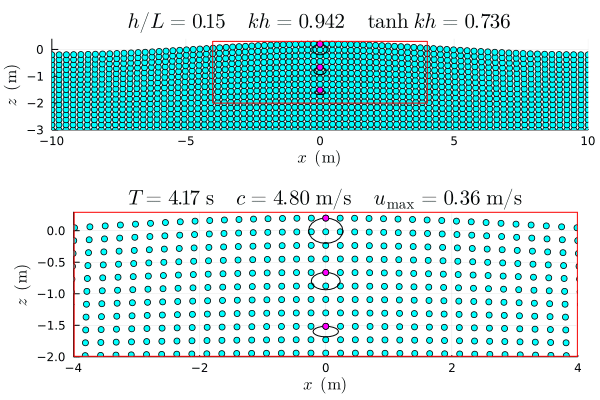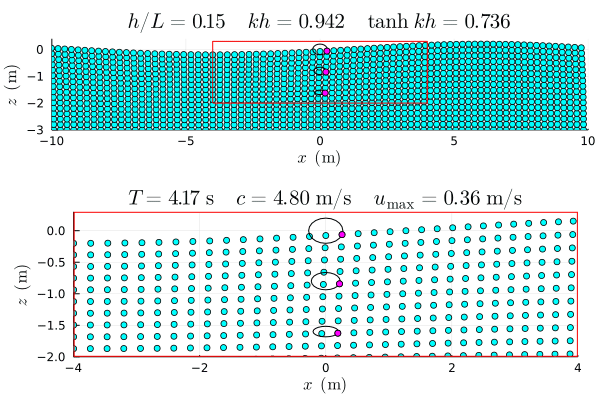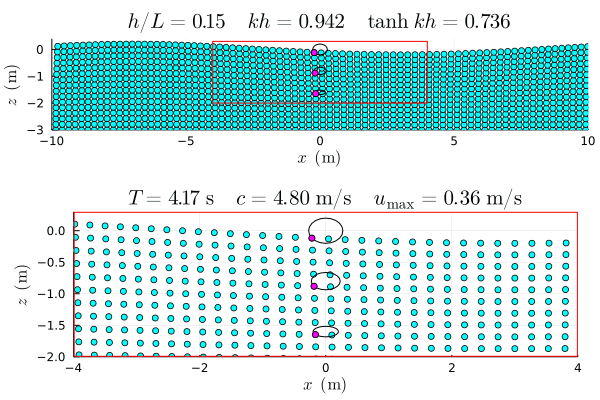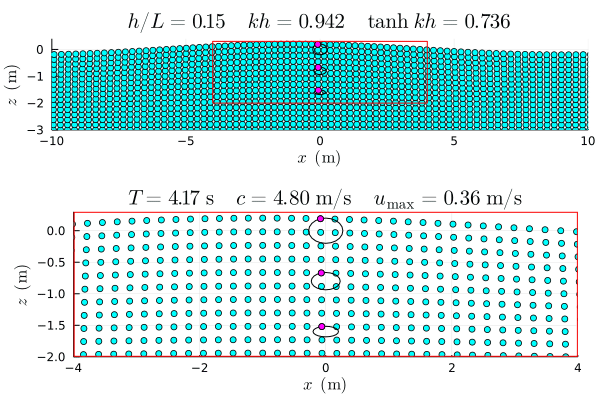
参考図 †
アニメーションは Julia で作成した gif.
深海波 †
浅海波 †
極浅海波(長波) †