(水面波の)線形分散関係 †
「分散関係」? †
微小振幅波理論における分散関係式 (dispersion relation)
\[
\omega^2 = gk\tanh kh \tag{1}
\]
は海岸工学の教科書で必ず出てくるが,この分散関係というのが何を意味するのか最初はよくわからなかったので,導出とともにメモ.
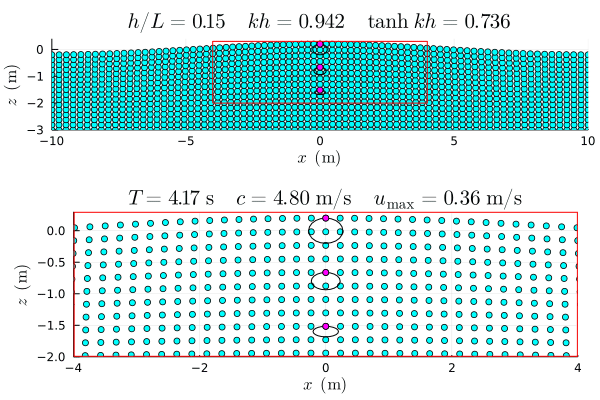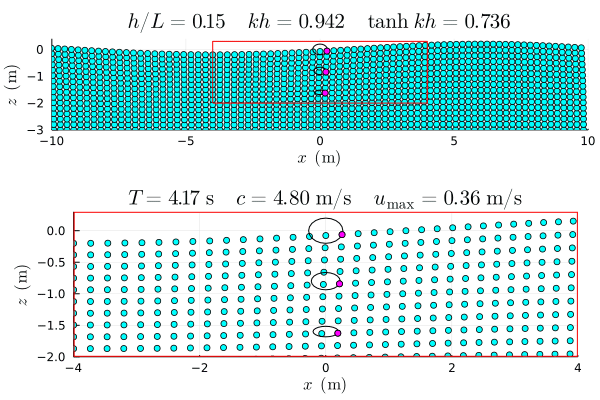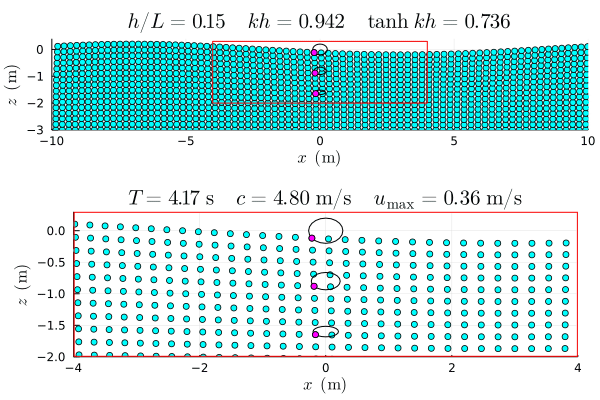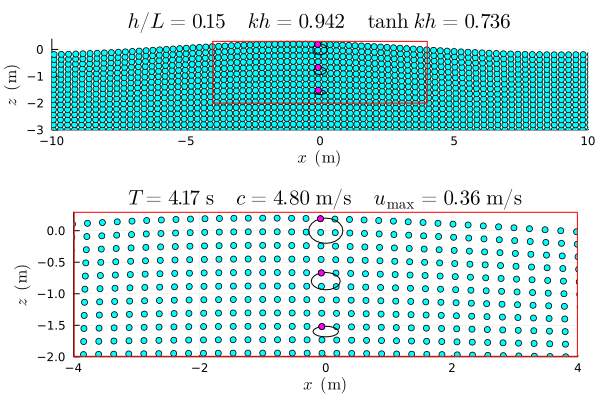
なお分散関係式といっても,水の波に限らずあらゆる種類のあらゆる分散関係式がある.
ここでは水面の微小振幅波(復元力は重力)の分散関係の話.
微小振幅波の分散関係式の導出 †
基礎方程式 †
まず基礎方程式と微小振幅波の境界条件を決める.
一様水深 \(h\) の水域を考え,波の進行方向に \(x\),水面から鉛直上向きに \(z\) 軸をとる.
渦なし流れを仮定すると,速度ポテンシャル \(\phi\) が存在し,水粒子の速度成分 \(u,w\) は次のように表される.
\[\begin{align}
u = \frac{\partial \phi}{\partial x} \tag{2} \\
w = \frac{\partial \phi}{\partial z} \tag{3} \\
\end{align}\]
ここでは水(海水)を非圧縮として扱うため,連続式は
\[\begin{align}
\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z} = 0 \tag{4}
\end{align}\]
となる.式(2)〜(4)より
\[\begin{align}
\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial z^2} = 0 \tag{5}
\end{align}\]
を得る(ラプラス方程式).これが非回転・非圧縮の流れの支配方程式であり,この関係は \(-h\le z \le \eta, -\infty \lt x \lt \infty \) の領域で成立していなければならない.
この支配方程式を満たす未知関数 \(\phi\) は無数に存在する.解の形をある程度仮定した上で境界条件を満たすものを求めることで,波の性質を持った \(\phi\) が定まっていく.
境界条件 †
海底での境界条件を考える.
水平な海底においては速度の鉛直成分は 0 でなければならないから,
\[
w = \frac{\partial \phi}{\partial z}=0,~\mathrm{for}~ z=-h\tag{6}
\]
を満たす必要がある.
次に水面での境界条件として,渦なし流れの運動方程式の積分形であるベルヌーイ式(圧力方程式)を書くと,
\[
\frac{\partial \phi}{\partial t} +
\frac{1}{2}\left[ \left( \frac{\partial \phi}{\partial x}\right)^2 + \left( \frac{\partial \phi}{\partial z}\right)^2\right]+\frac{p}{\rho}+gz = 0 \tag{7}
\]
ここで \(t\) は時間,\(p\) は圧力,\(\rho\) は水の密度,\(g\) は重力加速度.
自由表面 \(z=\eta\) での圧力を \(p_0\) とすれば,式(7) を用いて
\[
\frac{\partial \phi}{\partial t} +
\frac{1}{2}\left[ \left( \frac{\partial \phi}{\partial x}\right)^2 + \left( \frac{\partial \phi}{\partial z}\right)^2\right] +\frac{p_0}{\rho}+g\eta = 0,~\mathrm{for}~ z=\eta \tag{8}
\]
となる.
また,自由表面が \(F(x,z,t)=0\) のように表されるとすれば,境界上の水粒子は常に境界上に留まる.
これより,\(F\) の物質微分(ラグランジュ微分)は0でなければならない.よって,
\[
\frac{DF}{Dt} = \frac{\partial \eta}{\partial t} + u\frac{\partial \eta}{\partial x} - w = 0,~\mathrm{for}~ z=\eta
\]
\(u,v\) を \(\phi\) に置き換えると次のようになる.
\[
\frac{\partial \eta}{\partial t} + \frac{\partial \phi}{\partial x}\frac{\partial \eta}{\partial x} - \frac{\partial \phi}{\partial z} = 0,~\mathrm{for}~ z=\eta \tag{9}
\]
微小振幅波の仮定 †
ここまで
- 一様水深
- 非圧縮
- 非回転
- 非粘性
を仮定した.この仮定のもとで,
連続式と速度ポテンシャルによって得たラプラス方程式の式(5)
\[\begin{align}
\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial z^2} = 0 \tag{5}
\end{align}\]
および底面での境界条件式(6)
\[
\frac{\partial \phi}{\partial z}=0,~\mathrm{for}~ z=-h\tag{6}
\]
および水表面での境界条件式(8),(9)
\[\begin{align}
\frac{\partial \phi}{\partial t} +
\frac{1}{2}\left[ \left( \frac{\partial \phi}{\partial x}\right)^2 + \left( \frac{\partial \phi}{\partial z}\right)^2\right] +\frac{p_0}{\rho}+g\eta = 0,~\mathrm{for}~ z=\eta \tag{8}\\
\frac{\partial \eta}{\partial t} + \frac{\partial \phi}{\partial x}\frac{\partial \eta}{\partial x} - \frac{\partial \phi}{\partial z} = 0,~\mathrm{for}~ z=\eta \tag{9}\\
\end{align}\]
を満足する解を求めることになる.
このまま解こうとすると,式(8),(9)は非線形であるから非線形問題の解を求めることになる.
しかし,波高が波長 \(L\) または水深 \(h\) に比して非常に小さいと追加で仮定すれば,微小振幅の近似が可能で,線形に置き換えられる.
ということで微小振幅波を考え,\(\left.\dfrac{\partial \phi}{\partial t}\right|_{z=\eta}\) すなわち \(\dfrac{\partial}{\partial t} \phi(x,\eta,t)\) を \(z=0\) のまわりでテイラー展開すると
\[\begin{align}
\frac{\partial}{\partial t} \phi(x,0+\eta,t) = \frac{\partial}{\partial t} \phi(x,0,t) + \frac{\eta}{1}\frac{\partial}{\partial z}\frac{\partial}{\partial t} \phi(x,0,t) + \frac{\eta^2}{2!}\frac{\partial^2}{\partial z^2}\frac{\partial}{\partial t} \phi(x,0,t) + \cdots
\end{align}\]
ここから微小量の2次以上の項を無視して
\[\begin{align}
\left.\frac{\partial \phi}{\partial t}\right|_{z=\eta} \approx \left.\frac{\partial \phi}{\partial t}\right|_{z=0}
\end{align}\]
となる.同様に
\[\begin{align}
\left.\frac{\partial \phi}{\partial z}\right|_{z=\eta} \approx \left.\frac{\partial \phi}{\partial z}\right|_{z=0}
\end{align}\]
となる.これを境界条件の式(8),(9) に代入して,同様に2次以上の項を無視すると,以下のように書き換えられる.
\[\begin{align}
\frac{\partial \phi}{\partial t} + g\eta &= 0,~\mathrm{for}~ z=0 \tag{10}\\
\frac{\partial \eta}{\partial t} - \frac{\partial \phi}{\partial z} &= 0,~\mathrm{for}~ z=0 \tag{11}\\
\end{align}\]
ここで,水表面での大気の圧力 \(p_0\) を基準とし,\(p_0 = 0\) とおいた.
式(10),(11) より\(\eta\) を消去すると
\[\begin{align}
\frac{\partial^2 \phi}{\partial t^2} + g\frac{\partial \phi}{\partial z} = 0,~\mathrm{for}~ z=0 \tag{12}
\end{align}\]
を得る.
微小振幅波の分散関係式の導出 †
これまで導出した基礎式
\[\begin{align}
\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial z^2} = 0 \tag{5} \\
\end{align}\]
および境界条件の式
\[\begin{align}
\frac{\partial \phi}{\partial z}&=0 ,~\mathrm{for}~ z=-h\tag{6} \\
\frac{\partial^2 \phi}{\partial t^2} + g\frac{\partial \phi}{\partial z} & = 0 ,~\mathrm{for}~ z=0 \tag{12}
\end{align}\]
と変数分離法を使って分散関係式を求める.
未知関数 \(\phi\) の解の形として,\(x,z,t\) それぞれ独立した関数の積で表せることを仮定する.式で書けば次式の通り.
\[\begin{align}
\phi(x,z,t) = X (x)Z(z)T(t)
\end{align}\]
ここで \(X,Z,T\) はそれぞれ \(x,z,t\) だけの関数.さらに,時間的に周期性をもつ波を仮定すれば,
\[\begin{align}
\phi(x,z,t) = X (x)Z(z)e^{-i\omega t} \tag{13}
\end{align}\]
とおける.ここで,\(\omega\) は角周波数.\(e^{-i\omega t}\) は \(e^{i\omega t}\) とおいてもよいし,実部だけを見るなら \(\mathrm{Re}~e^{i\theta} = \cos\theta\) であるから \(\cos\omega t\) とおいてもよい.得られる分散関係式は結局同じものになる.
また,\(x\) 方向の進行する波の向きも限定して解の形を仮定し,\(X(x)T(t) = \sin(kx-\omega t)\) とおくこともできる.
今回は式変形上扱いやすく,より汎用的になるよう \(T(t) = e^{-i\omega t}\) とする.
式(13)をラプラスの式,式(5)に代入して
\[\begin{align}
X^{\prime\prime}Ze^{-i\omega t} + XZ^{\prime\prime}e^{-i\omega t} = 0
\end{align}\]
両辺を \(XZe^{-i\omega t}\) で割って
\[\begin{align}
\frac{X^{\prime\prime}}{X} + \frac{Z^{\prime\prime}}{Z} &= 0 \\
\frac{Z^{\prime\prime}}{Z} &= -\frac{X^{\prime\prime}}{X} \tag{14}
\end{align}\]
この式(14)の左辺は仮定した通り \(Z\) だけの関数,右辺は \(X\) だけの関数である.
この式が恒等的に成立するためには,両辺がある定数でなければならない.
( \(x\) だけ,\(z\) だけ変化した場合にも成立しなければならないため.)
そこである定数 \(k>0\) を用いて
\[\begin{align}
\frac{Z^{\prime\prime}}{Z} = -\frac{X^{\prime\prime}}{X} = k^2 \tag{15}
\end{align}\]
とする.\(Z\) の項と \(X\) の項は符号だけ逆の関係であり,\(\dfrac{Z^{\prime\prime}}{Z}=-\dfrac{X^{\prime\prime}}{X} = k^2\) とするか \(\dfrac{Z^{\prime\prime}}{Z}=-\dfrac{X^{\prime\prime}}{X} = -k^2\) とするかで話が変わってくる.
一方は双曲線関数を解に持ち,他方は三角関数を解に持つことは式から明らかだが,この時点ではどっちがどっちなのかまだ決まっていない.
本当は
\[\begin{align}
\frac{Z^{\prime\prime}}{Z} = -\frac{X^{\prime\prime}}{X} = \alpha
\end{align}\]
とおいて,\(\alpha>0,~\alpha=0,~\alpha<0\) のそれぞれの条件で境界条件を満たす \(\phi\) があるかを確認し,\(\alpha>0\) の時だけが物理的な拘束を満たすことを確認した上で,
\[\begin{align}
\frac{Z^{\prime\prime}}{Z} = -\frac{X^{\prime\prime}}{X} = k^2 \tag{15}
\end{align}\]
とおくのが正攻法.ここでは面倒くさいので省略.
ただ,\(x,\,z\) 方向のどちらが\(\sin, \cos\),つまりは \(e^{ikx}\) のように周期的な解でどちらが\(\sinh, \cosh\,(e^{kz})\)の形の解になるか想像はつく.
式(15)より,定数 \(A,B,C,D\) を用いて \(Z,X\) を表すと
\[\begin{align}
Z &= Ae^{kz} + Be^{-kz} \tag{16}\\
X &= Ce^{ikx} + De^{-ikx} \tag{17}\\
\end{align}\]
となる(分散関係式を求めるにあたっては,\(X\) は \(X\) のままでもOK).
これより \(\phi\) を書き直すと
\[\begin{align}
\phi(x,z,t) &= X (x)Z(z)e^{-i\omega t} \tag{13}\\
\phi(x,z,t) &= \left(Ae^{kz} + Be^{-kz}\right) \left(Ce^{ikx} + De^{-ikx}\right)e^{-i\omega t} \tag{18}\\
\end{align}\]
となる.解の形を仮定し,ラプラス方程式に代入して得た式(18)を,境界条件を表す式(6)および式(12)に代入すると次の式(19),(20)を得る.
\[\begin{align}
e^{-kh}A - e^{kh}B &= 0 \tag{19}\\
(\omega^2-gk)A + (\omega^2+gk)B &= 0 \tag{20}\\
\end{align}\]
式(19),(20)を行列にして書くと次のようになる.
\[
\left(
\begin{array}{cc}
e^{-kh} & -e^{kh} \\
\omega^2-gk & \omega^2+gk \\
\end{array}
\right)
\left(
\begin{array}{c}
A \\
B \\
\end{array}
\right) =
\left(
\begin{array}{c}
0 \\
0 \\
\end{array}
\right)
\tag{21}
\]
\(A,B\) がともに0でない非自明解をもつためには係数行列の行列式が0でなければならない.
(逆行列が存在した場合,式(21)に係数行列 \(P\) の逆行列 \(P^{-1}\) を左からかけると \(A = B = 0\) となるため.)
したがって解が存在する条件として
\[
\left|
\begin{array}{cc}
e^{-kh} & -e^{kh} \\
\omega^2-gk & \omega^2+gk \\
\end{array}
\right| = 0 \tag{22}
\]
が得られ,これを解くと
\[\begin{align}
(\omega^2+gk)e^{-kh} + (\omega^2-gk)e^{kh}&= 0 \\
(e^{kh}+e^{-kh})\omega^2 - (e^{kh}-e^{-kh})gk &= 0 \\
\end{align}\]
より
\[\begin{align}
\omega^2 &=gk\frac{e^{kh}-e^{-kh}}{e^{kh}+e^{-kh}} \\
&=gk\tanh kh \tag{23}\\
\end{align}\]
となり,最初に示した分散関係式を得る.
分散関係式の解釈 †
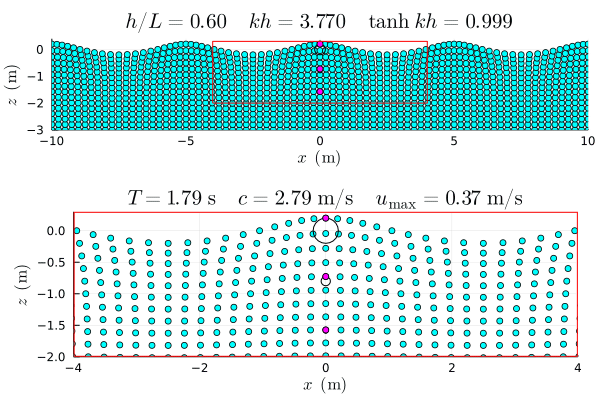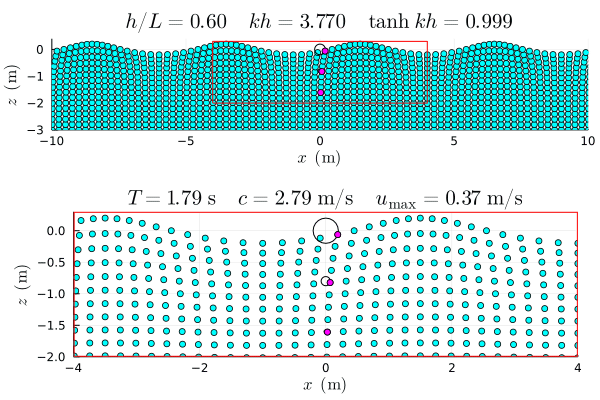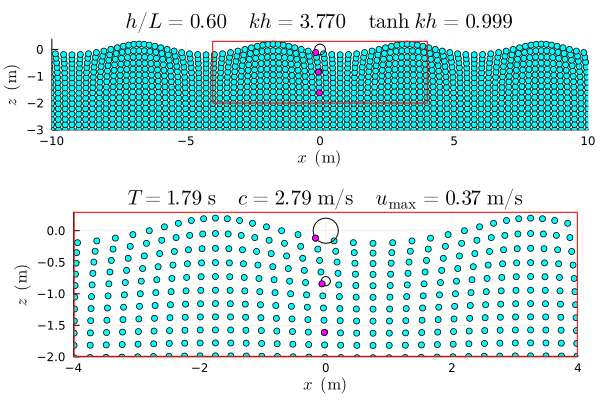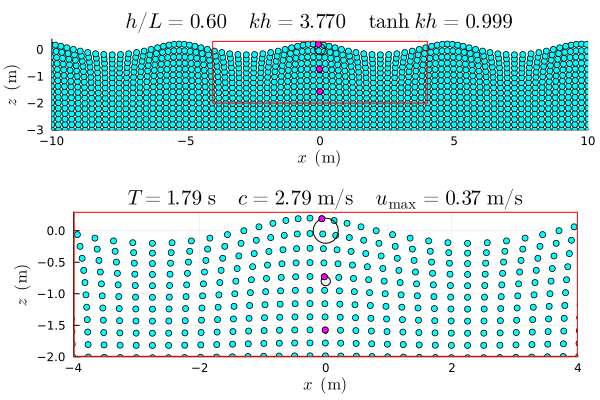
水面波の挙動の支配方程式を満たすためには, 一般に角振動数 \(\omega\) と波数 \(k\) は独立ではなく,分散関係式である式(23)の通り,相互に関係付けられている.
「分散関係」という言葉は,波速(位相速度)\(c=\omega/k\) を考えるとわかりやすい.
\(\omega\) は \(k\) の関数であるから,波速 \(c\) も波数 \(k\) に,つまり波長 \(L\) に依存する.
フーリエ解析によれば,任意の波形は様々な波長の正弦波の重ね合わせで表現できる.したがって,\(c\) が \(L\) に依存する場合,どのような初期波形であってもそれぞれの波長の波が異なる速さで伝播していくため,波形は時間の経過とともに波長ごとに散らばっていく(分散する)ことになる.
このように \(c\) が一定でなく \(k\) に依存する(\(c(k)\) となる)ような波動を「分散性」波動という.