Lotka-Volterra方程式 メモ †
ロジスティック方程式を2変数に拡張したもの.
\[ \begin{align}
{dx \over dt} = \varepsilon_1 x - k_1xy \tag{1} \\
{dy \over dt} = -\varepsilon_2 y + k_2xy \tag{2}
\end{align}
\]
\(x\) を草食動物の個体数,\(y\) を肉食動物の個体数として生態系の変化を表す(簡略な)モデルの代表.
草食動物は草を食べて増殖 \(+\varepsilon_1 x\)するが,肉食動物に遭遇すると一定の割合で食べられて個体数は減少する.
各々の個体数が増えるほど遭遇率は高くなり(\(k_1xy\)),遭遇すると草食の場合は個体が減るので \( -k_1xy \) になる.
逆に肉食動物は草食動物を食べることで個体数を増やし(\( +k_2xy\)),自然死などの理由で減少する(\(-\varepsilon_2 y\)).
安定サイクルに入るようなパラメータの組み合わせはかなり限定的で難しい.
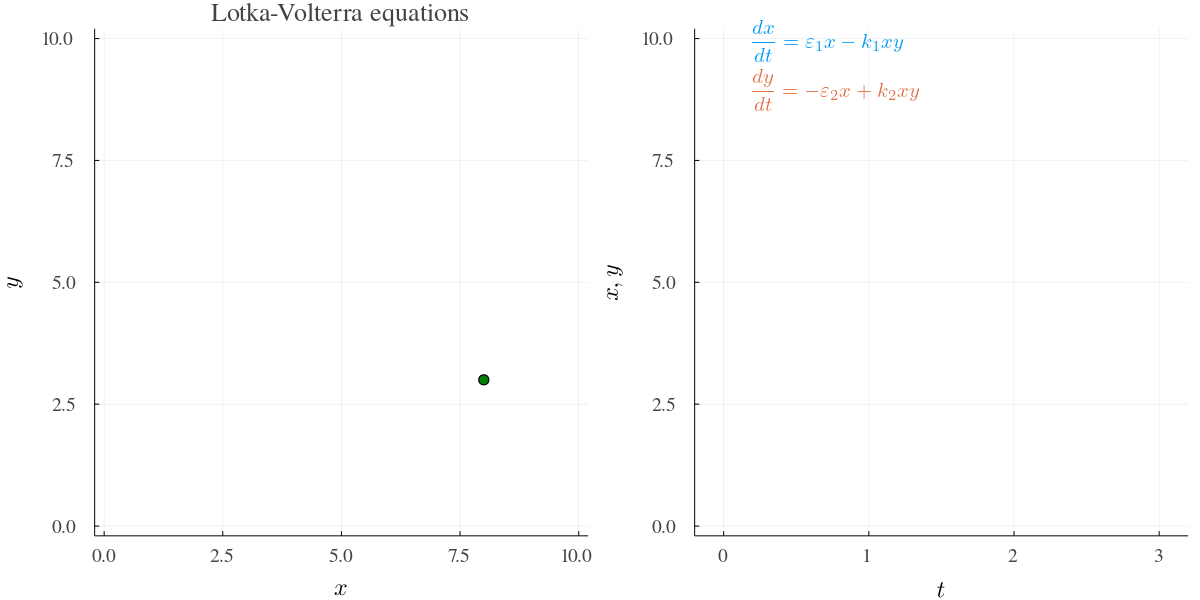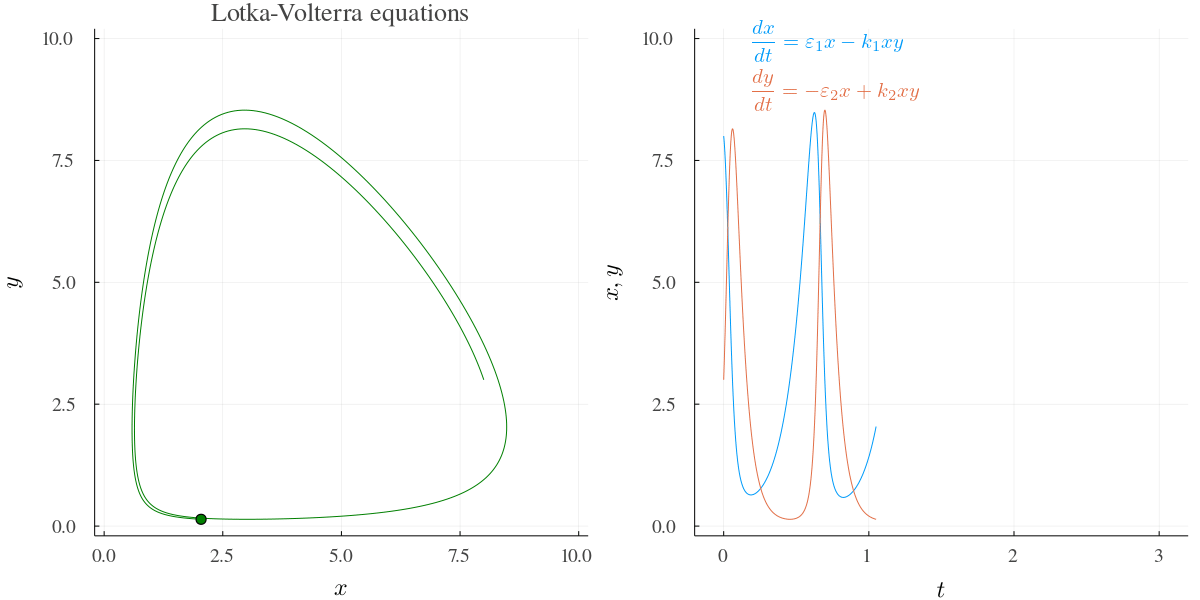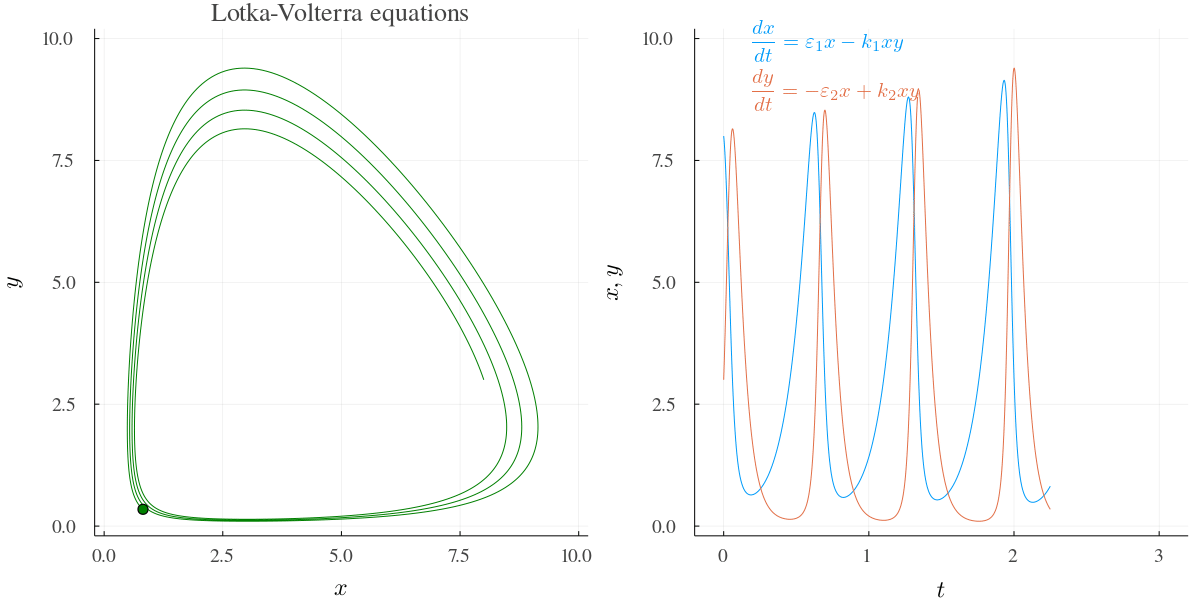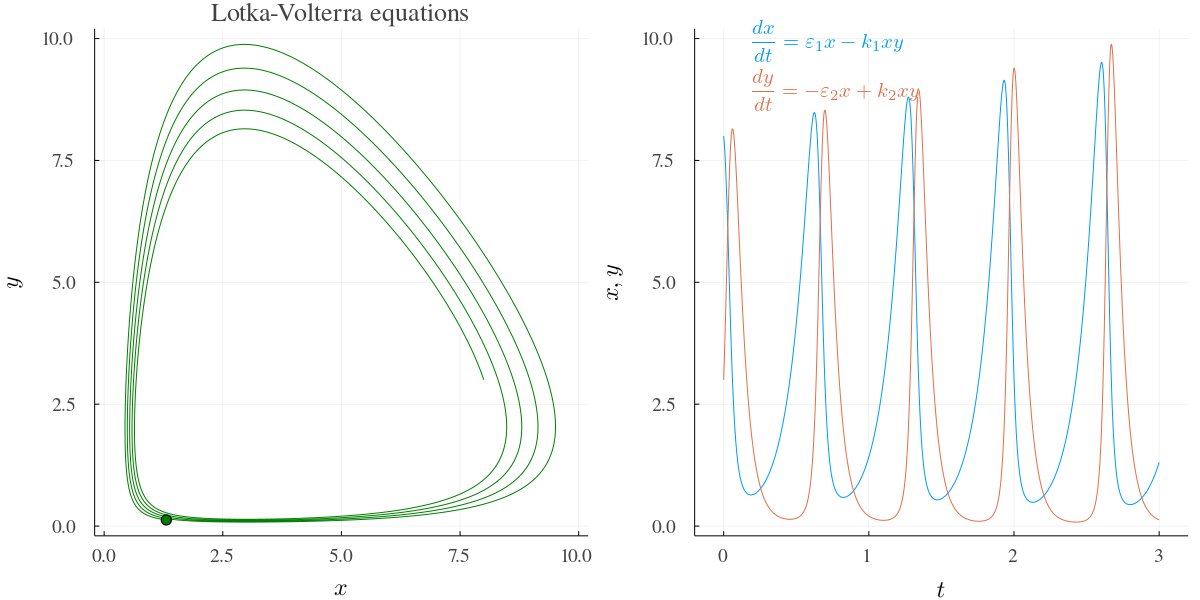
下の図は Julia で解いてみた例.このあと個体数 \(x,y\) は爆発する.