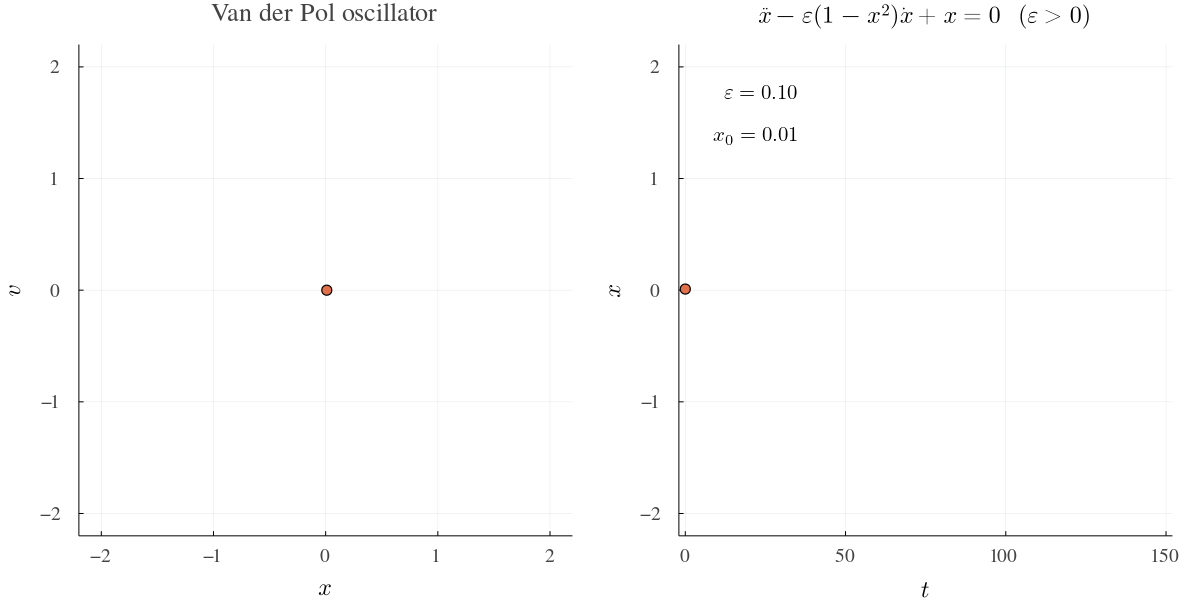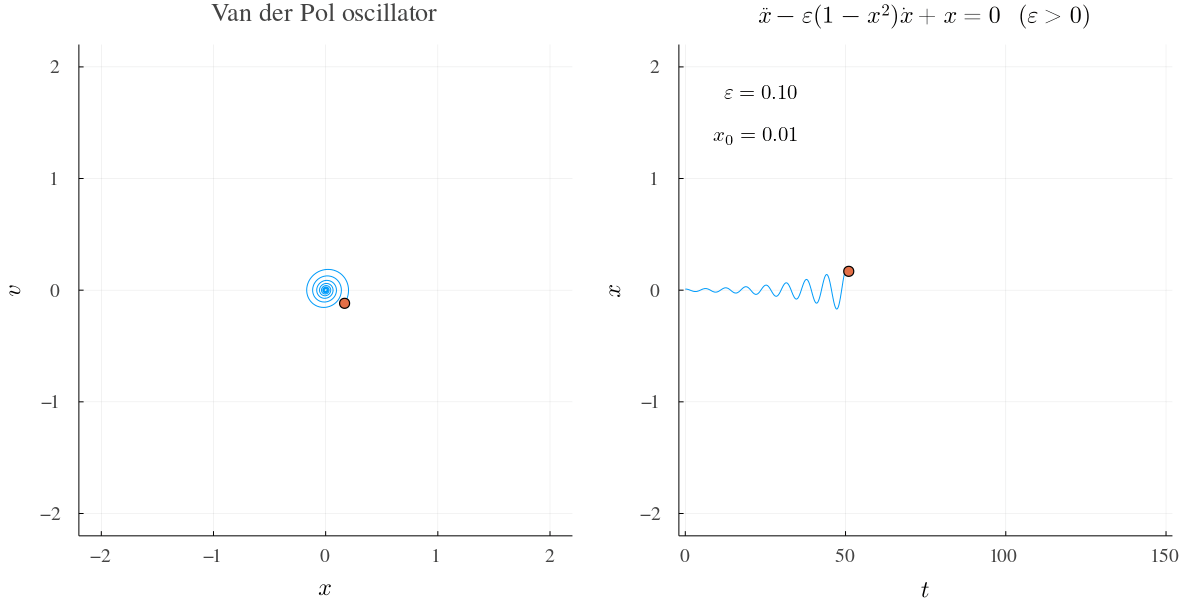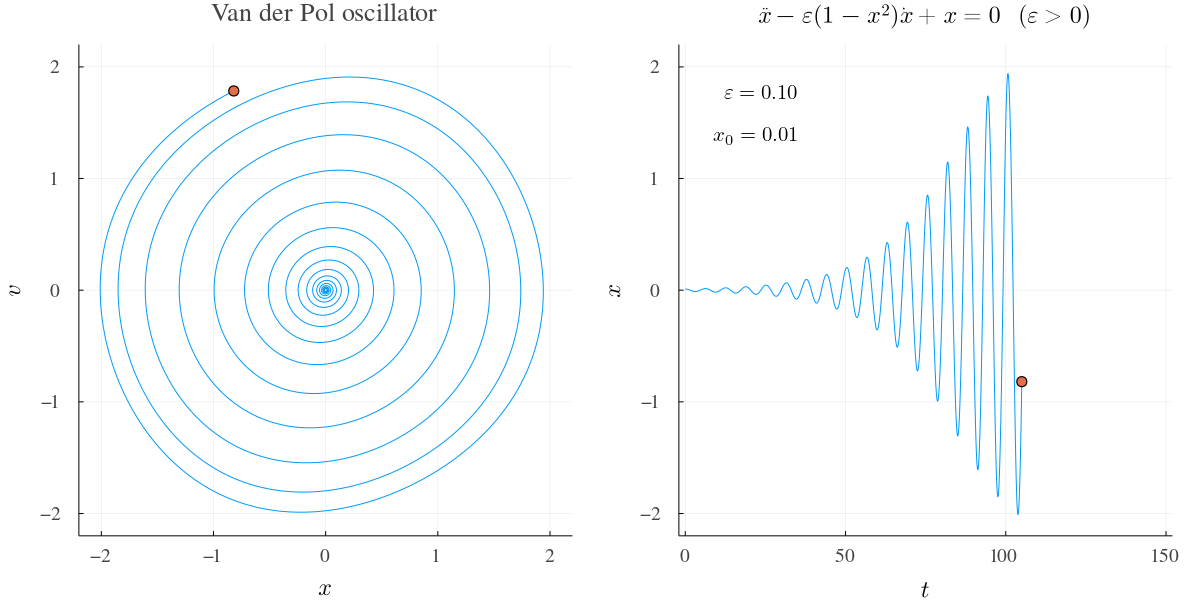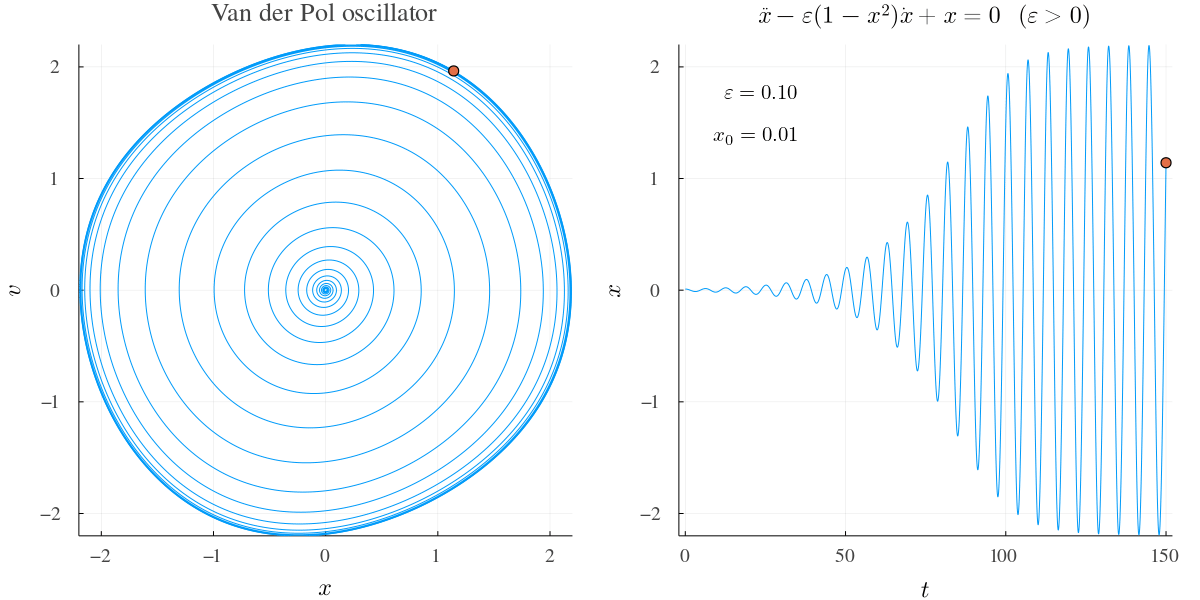Van der Pol 振動子 メモ †
式 †
\[ \
{d^{2}x \over dt^{2}}-\varepsilon (1-x^{2}){dx \over dt}+x=0 \,\, (\varepsilon>0) \tag{1}\
\]
左辺第2項の速度に比例した負抵抗(\( -\varepsilon \))によって徐々に振動が成長する.
例1 †
\(\varepsilon\) が小さいときの挙動.
左図は \(v-x\) 図で右は \(x-t\) 図.
徐々に振幅が大きくなっていくが,第2項の \( 1-x^2 \) の効果も強まって振幅はやがて落ち着く.
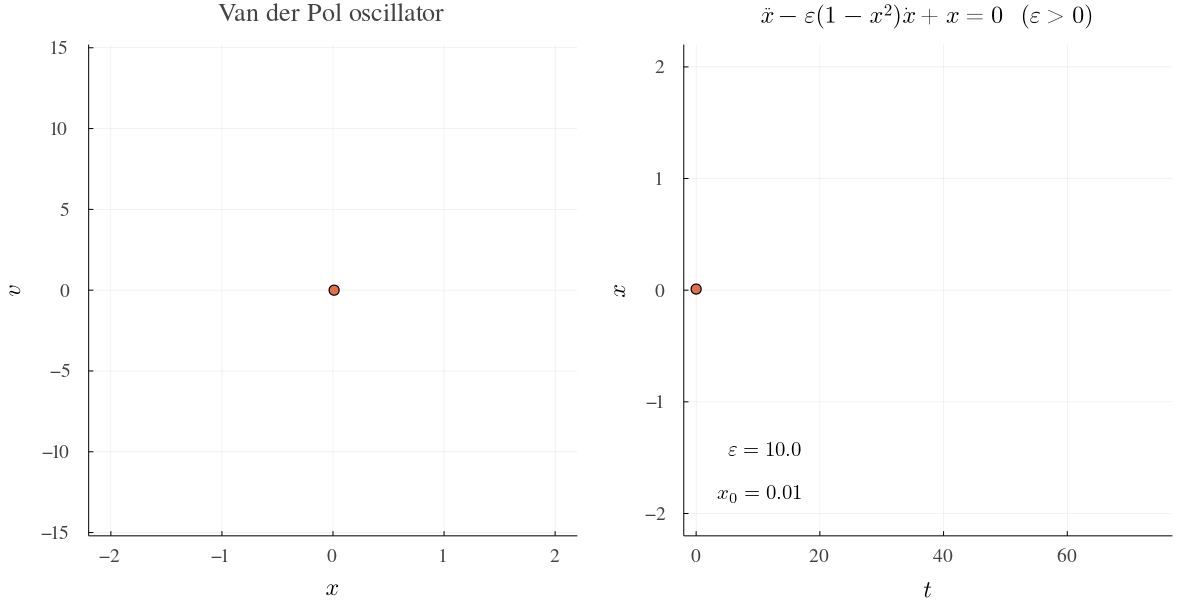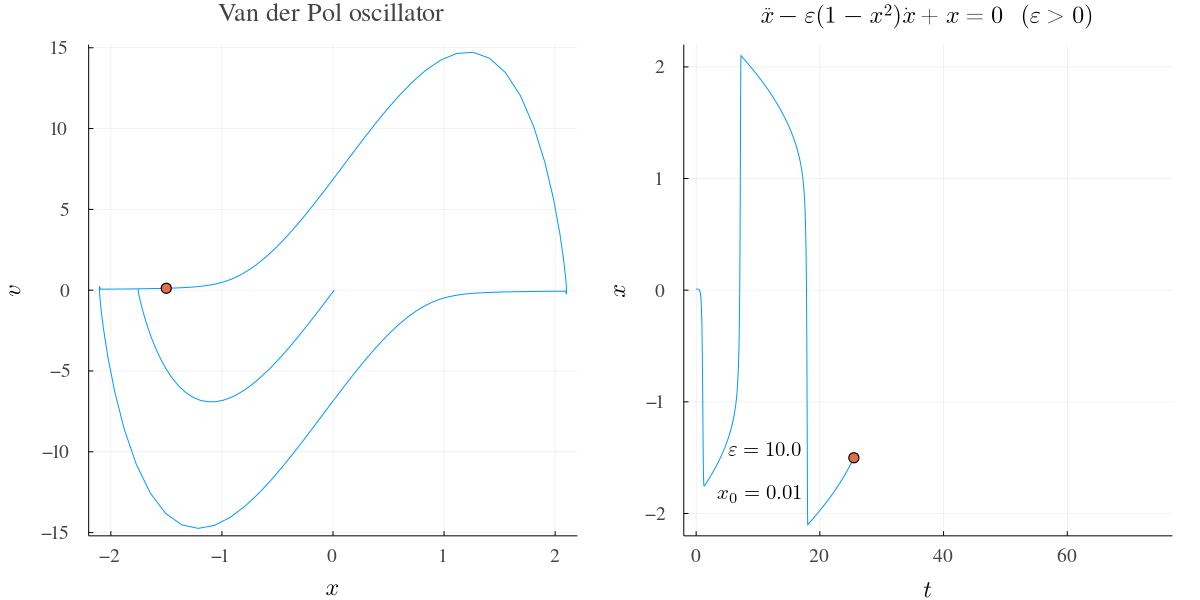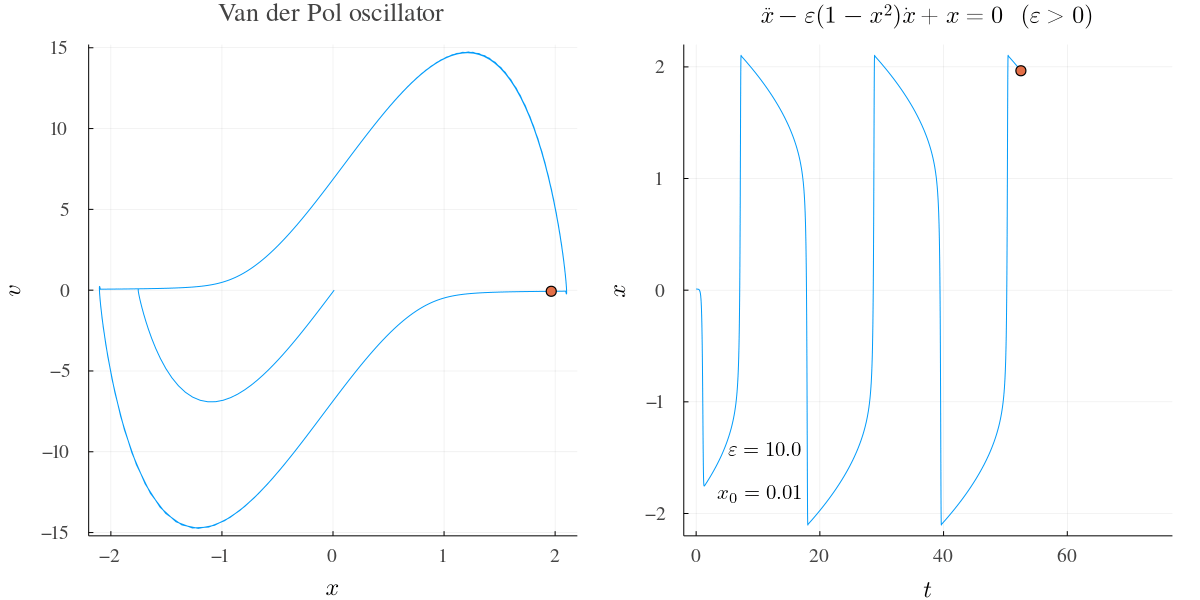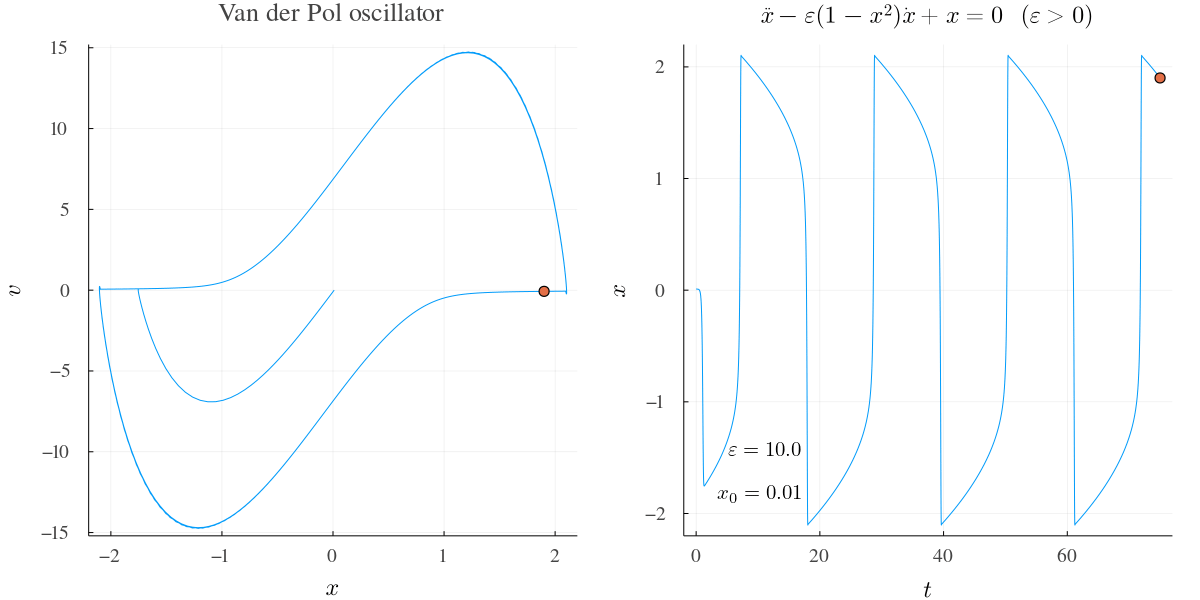
例2 †
\(\varepsilon\) が大きいときの挙動.
開始すぐ定常サイクルにはまって以降同じ振動を繰り返す.