波動方程式 †
1次元の波動 †
次式で表される波動方程式を満たす\(\phi(\boldsymbol{x},t) \)
\[
\frac{\partial^2 \phi}{\partial t^2} - c^2 \nabla^2 \phi = 0 \tag{1}
\]
を数値的に解く.ここで,\(\boldsymbol{x}, t\)は空間,時間を表す量, \(c\) は波速(一定)である.
上式が空間的に1次元の場合,波動方程式は
\[ \frac{\partial^2 \phi}{\partial t^2} - c^2\frac{\partial^2 \phi}{\partial x^2} = 0 \tag{2}\]
となる.
解 †
1次元の式(2)は,数学的にこのような書き方が許されるかはわからないが,
\[ \left(\frac{\partial }{\partial t} - c\frac{\partial }{\partial x} \right)\left(\frac{\partial }{\partial t} + c\frac{\partial }{\partial x} \right) \phi = 0 \tag{3}\]
と表せる.カッコの中は \(\phi\) を含まないただの演算子なので注意.これは
\[ \left(\frac{\partial \phi}{\partial t} - c\frac{\partial \phi}{\partial x} \right) = 0 \tag{4} \]
または
\[ \left(\frac{\partial \phi}{\partial t} + c\frac{\partial \phi}{\partial x} \right) = 0 \tag{5} \]
となる.これらの式は1次元の移流方程式であり,式(4)と式(5)はぞれぞれ逆の方向への移流を指す.
したがって,1次元の移流方程式は同時に1次元の波動方程式の解(のひとつ)になる.
何らかの初期条件が与えられたとすれば,\(\phi\) の挙動は
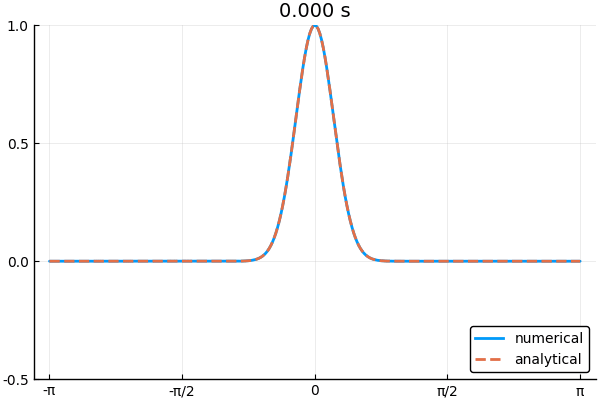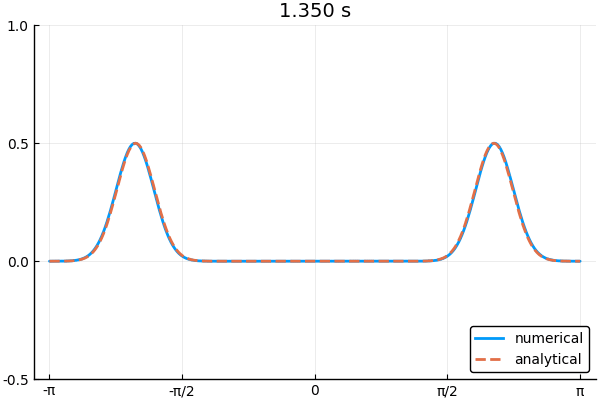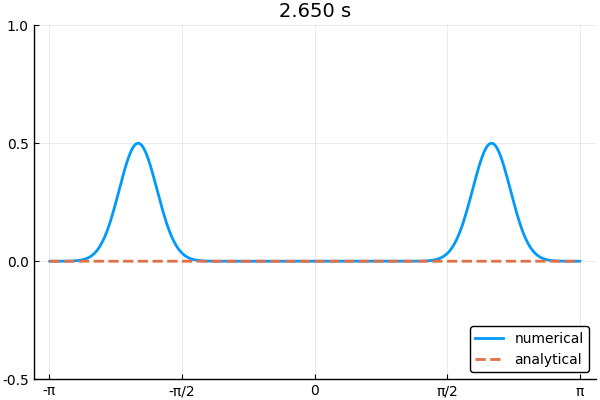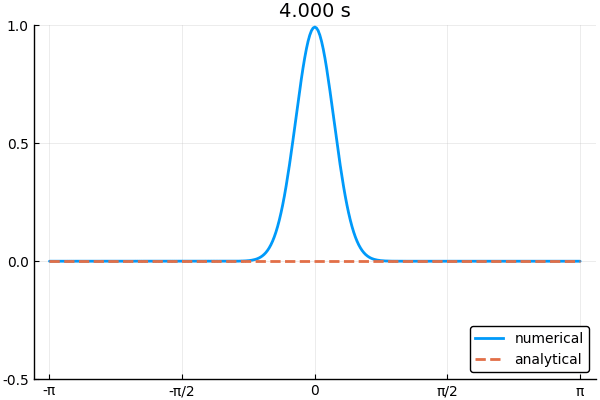
\[ \phi(x,t) = \frac{1}{2}\phi(x-ct,0) + \frac{1}{2}\phi(x+ct,0) \tag{6} \]
となる.
数値計算 †
最も簡単な1次元のこの形式で数値的に解くことを考える.
数値的に解くために,数式にあるような連続空間から離散空間へ落としこむ.
時間を固定して考えると, \(\phi(x\pm\Delta x)\) の値はテイラー展開を使って以下のように表せる.
\[\phi(x+\Delta x) = \phi(x) + \frac{\partial \phi(x)}{\partial x} \Delta x + \frac{1}{2} \frac{\partial^2 \phi(x)}{\partial x^2} (\Delta x)^2 + ... \tag{7}\]
\[\phi(x-\Delta x) = \phi(x) - \frac{\partial \phi(x)}{\partial x} \Delta x + \frac{1}{2} \frac{\partial^2 \phi(x)}{\partial x^2} (\Delta x)^2 - ... \tag{8}\]
高次の\(\Delta x\)の項を無視し,この2式を辺々足して整理すると
\[\frac{\partial^2 \phi(x)}{\partial x^2} = \frac{\phi(x+\Delta x) - 2\phi(x) + \phi(x-\Delta x)}{(\Delta x)^2} \tag{9} \]
を得る.\(\phi(x)\) を \(\phi_i\),\(x\) から正の方向に \(\Delta x\) だけ離れた点の\(\phi\)を \(\phi_{i+1}\) のように表記すると,
\[ \frac{\partial^2 \phi_i}{\partial x^2} = \frac{\phi_{i+1} - 2\phi_i + \phi_{i-1}}{(\Delta x)^2} \tag{10} \]
となる.
時間 \( t\) についても同様に離散化した \(j\) 番目の時刻を上付き添字 \(j\) で表すとすると,離散化した1次元波動方程式は次のように書ける.
\[ \frac{\phi^{j+1}_{i} - 2\phi^{j}_{i} + \phi^{j-1}_{i}}{(\Delta t)^2} = c^2 \left( \frac{\phi^{j}_{i+1} - 2\phi^{j}_{i} + \phi^{j}_{i-1}}{(\Delta x)^2} \right) \tag{11} \]
数値計算では,点 \(x_i\) で時間が \(\Delta t\) だけ進んだ値 \(\phi^{j+1}_{i}\) を逐次計算していくことになる.上式を \(\phi^{j+1}_{i}\) について解くと
\[ \phi^{j+1}_{i} = 2(1-\lambda^2)\phi^{j}_{i} + \lambda^2\left(\phi^{j}_{i+1} + \phi^{j}_{i-1} \right) - \phi^{j-1}_{i} \tag{12} \]
となる.ただし,
\[ \lambda^2 = \left( c \frac{\Delta t}{\Delta x} \right)^2 \tag{13} \]
である.式(12)の右辺は,格子上で隣接した\(\phi\)や前の時間の\(\phi\)など,4つの既知量,\( \phi^{j}_{i}, \phi^{j-1}_{i}, \phi^{j}_{i-1}, \phi^{j}_{i+1} \) と定数のみで構成されている.
したがって,順番にこの式をあてはめて計算することで,時間発展を数値的に解くことができる.
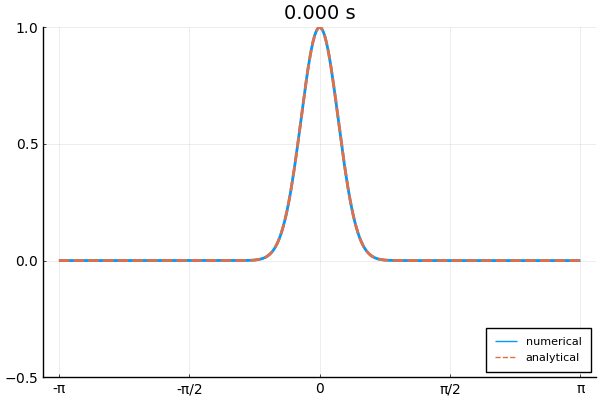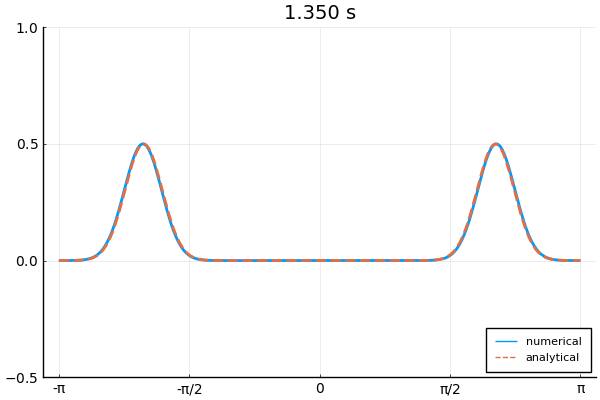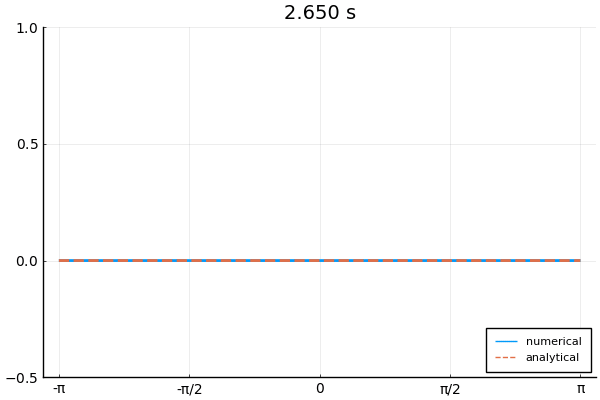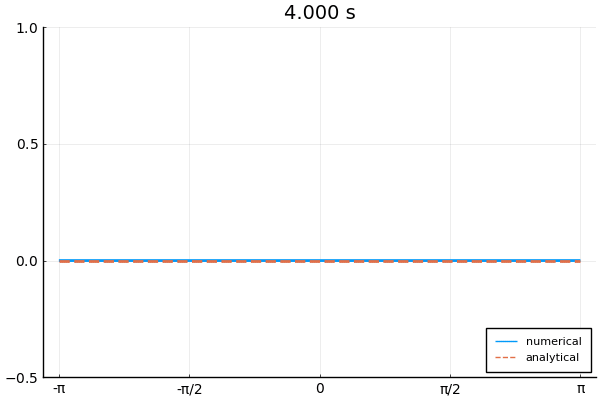
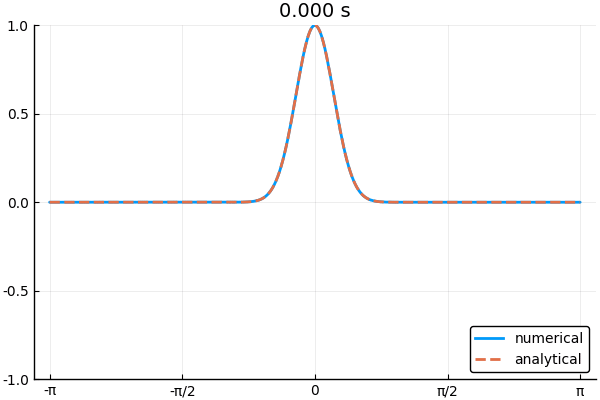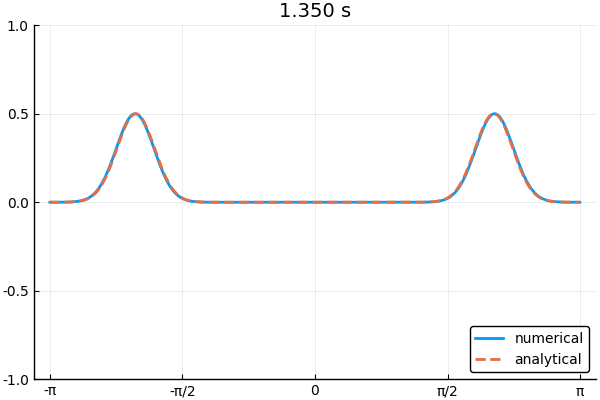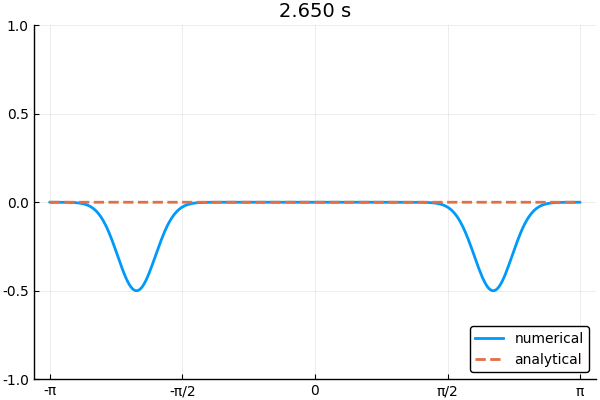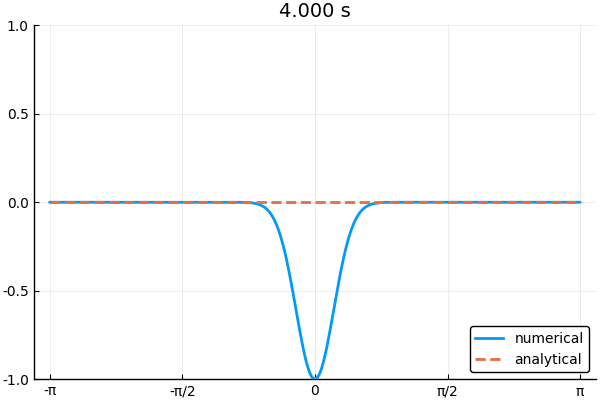
下の図は境界条件3つを使って1次元波動方程式を解いた例.