ベッセル関数 †
はじめに †
ベッセル関数は,ベッセルの微分方程式
\[
x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+(x^{2}-\nu ^{2})y=0
\]
を満たす \(y(x)\) の解.
少し見やすくなるように一部文字を変えて変形すると(数学的に色々問題があるのはさておき),
\[
\left[\frac{\partial^2}{\partial x^2}+\frac{1}{x}\frac{\partial}{\partial x}+\left(1-\frac{\nu^2}{x^2}\right)\right]Z_{\nu}(x) = 0
\]
となる.この \(Z_{\nu}(x)\) を次数 \(\nu\) のベッセル関数という.\(\nu\) は実数で,0 や正の整数 \(n\) のときは \(n\) 次ともいう.
ベッセルの微分方程式は,例えば波動方程式を変数分離し直交座標系から円筒座標系に変換することで出てくる.
2次元のラプラシアン \(\nabla^2\) を極座標表示にすると
\[
\nabla^2 = \left(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} = \right) \frac{\partial^2}{\partial r^2} + \frac{1}{r}\frac{\partial}{\partial r} + \frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}
\]
であり,上式の右辺に着目すると,ベッセルの微分方程式っぽい要素が垣間見える.
波動方程式からベッセル微分方程式を得る過程は別ページに書いた.
次数 \(\nu\) が整数か非整数かの区別は必要だが,いずれにしてもベッセルの微分方程式では独立な解を2つ得られる.
その一方を第一種ベッセル関数 \(J_\nu\) とし,他方を 第ニ種ベッセル関数 \(N_\nu\) という.
したがって,最初の形式のベッセル微分方程式の一般解は,
\[
y(x) = AJ_\nu(x)+BN_\nu(x)
\]
と表せる.\(A,\,B\) は定数.
第一種ベッセル関数 \(J_\nu\) を単に(狭義の)ベッセル関数という場合もあるし,
これと区別するために第二種ベッセル関数 \(N_\nu\) はノイマン関数とも呼ばれる.
文献によってはノイマン関数は \(N_\nu\) でなくて \(Y_\nu\) とも書かれる.
さらに,これらの線型結合である
\[
H_\nu^{(1)}(x) = J_\nu + iN_\nu \\ H_\nu^{(2)}(x) = J_\nu - iN_\nu
\]
もベッセル微分方程式の解となり,前者を第一種ハンケル関数,後者を第二種ハンケル関数という.
ハンケル関数は第三種ベッセル関数ともいう(ややこしい).
\(J_\nu,\,N_\nu,\,H_\nu^{(1)},\,H_\nu^{(2)}\) を総称して(広義の)ベッセル関数,円柱関数といい,代表として \(Z_{\nu}\) と書かれる場合もある.
第一種ベッセル関数 \(J_\nu\) †
次数が整数の場合,第一種ベッセル関数 \(J_n\) は
\[
J_n(x) = \sum_{s=0}^\infty \frac{(-1)^s}{s!\,(s+n)!}\left(\frac{x}{2}\right)^{n+2s}
\]
である.次数 \(n\) を非整数も含めた実数領域 \(\nu\) へ拡張するには,階乗をガンマ関数 \(\Gamma(\cdot)\) に置き換えれば良いので,
\[
J_\nu(x) = \sum_{s=0}^\infty \frac{(-1)^s}{s!\,\Gamma(s+\nu+1)}\left(\frac{x}{2}\right)^{\nu+2s}
\]
となり,これが第一種ベッセル関数を表す基本的な式である.
整数次の第一種ベッセル関数 \(J_n(x)\) は下記のようになる.横軸が \(x\).
次数が大きくなるほど立ち上がりが遅くなり,振幅は \(\sqrt{x}\) に比例して減少する.
また,十分大きな \(x\) に関しては下記の式で近似できる.
\[
J_\nu(x) \approx \sqrt{\frac{2}{\pi x}}\cos\left(x-\frac{\pi\nu}{2}-\frac{\pi}{4}\right)
\]
どの程度大きくなれば近似が可能かは,下図を参照.
第二種ベッセル関数(ノイマン関数) \(N_\nu\) †
第ニ種ベッセル関数(ノイマン関数) \(N_\nu\) は, \[ N_\nu(x) = \frac{J_\nu(x) \cos\,\pi\nu - J_{-\nu}(x)}{\sin\,\pi\nu} \] で表せる.十分大きな \(x\) に対する近似式は下記の通り.\(J_\nu\) の近似式の \(\cos\) が \(\sin\) になっただけ. \[ N_\nu(x) \approx \sqrt{\frac{2}{\pi x}}\sin\left(x-\frac{\pi\nu}{2}-\frac{\pi}{4}\right) \] ノイマン関数 \(N_n(x)\) の概形は下図の通り.小さい \(x\) の範囲では下に伸びている.
また,(第一種)ベッセル関数とノイマン関数を並べて書くと次の通りで,\(x\) が大きくなるにつれて \(J_1\) と \(N_0\), \(J_2\) と \(N_1\) がそれぞれ重なっていく.
第三種ベッセル関数(ハンケル関数) \( H_\nu^{(1)},\,H_\nu^{(2)} \) †
ハンケル関数の定義は上にあるように
\[
H_\nu^{(1)}(x) = J_\nu + iN_\nu \\ H_\nu^{(2)}(x) = J_\nu - iN_\nu
\]
であり,式から明らかなように,プログラムを書く時は必ず複素数(Complex)型にする必要がある.
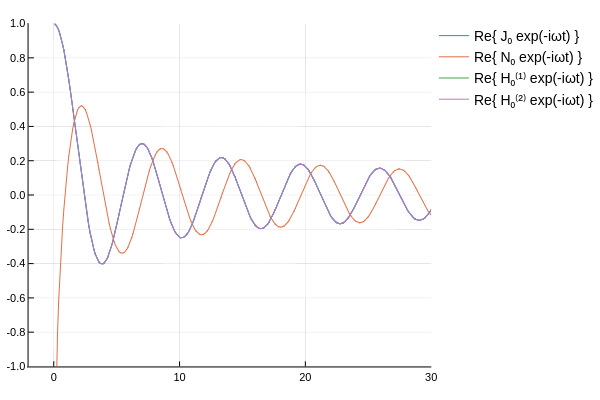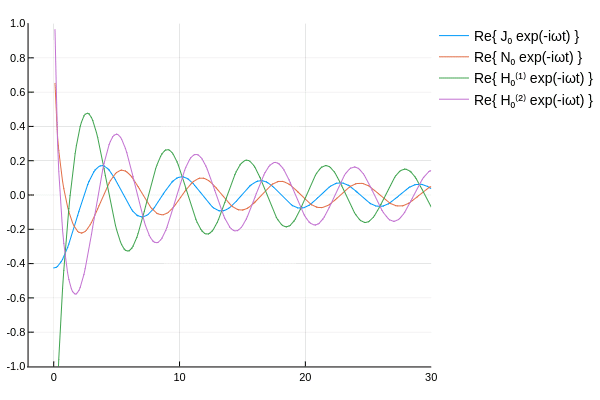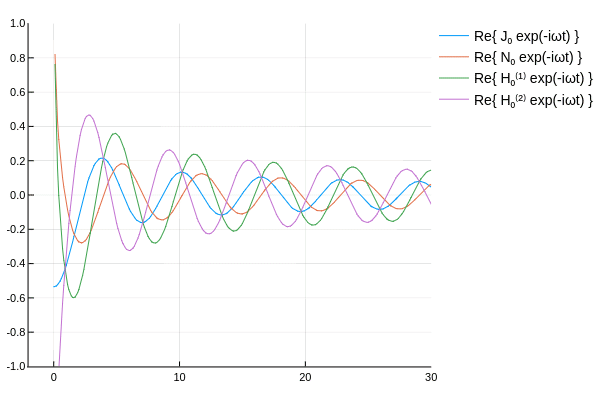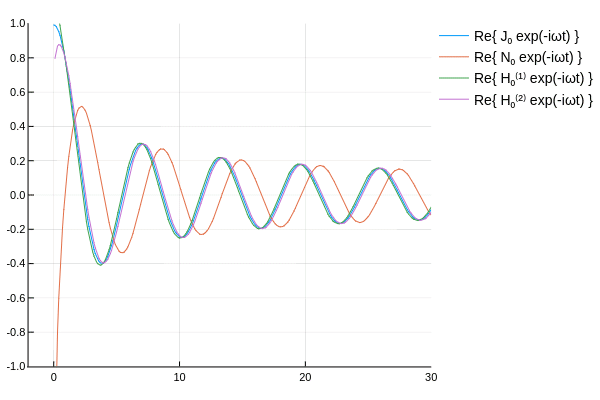
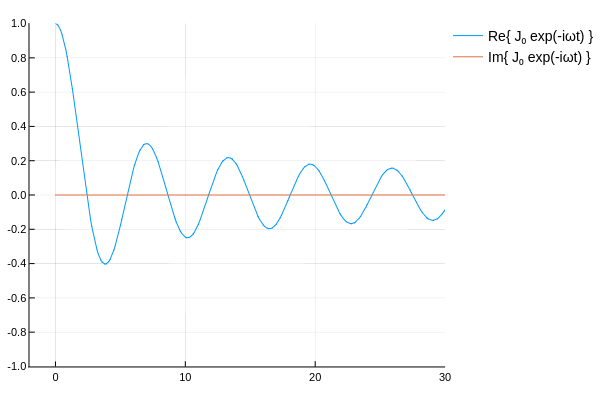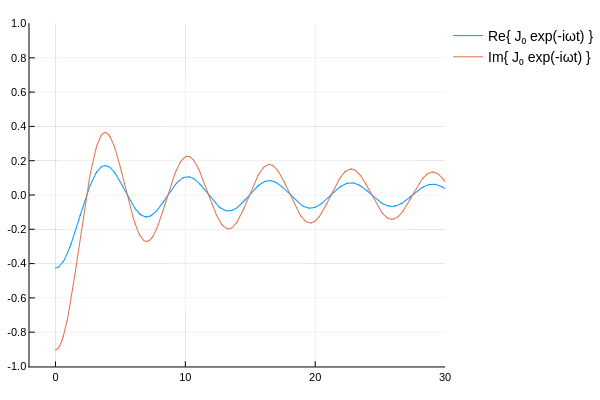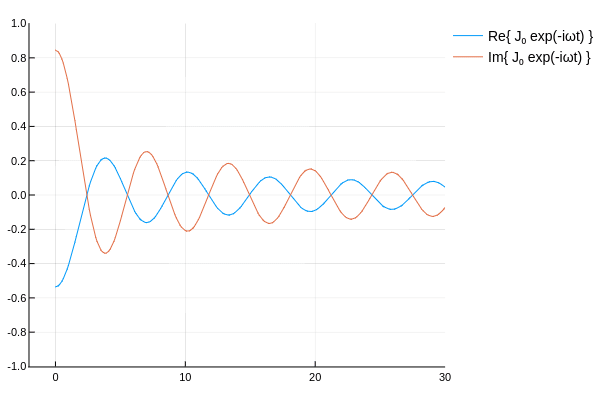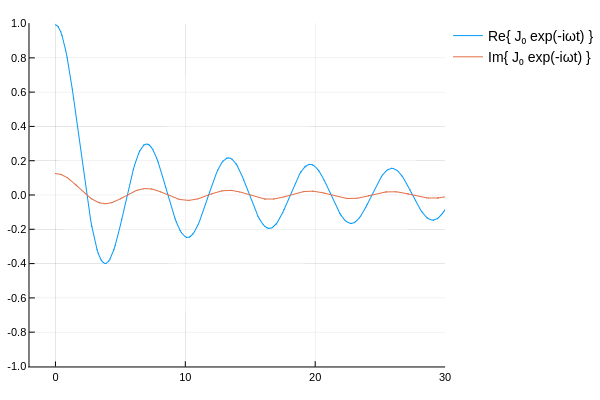
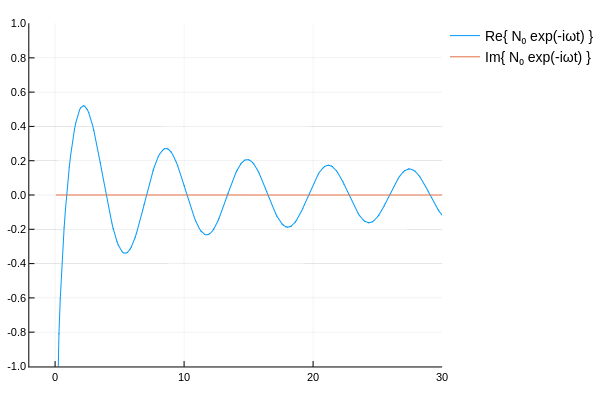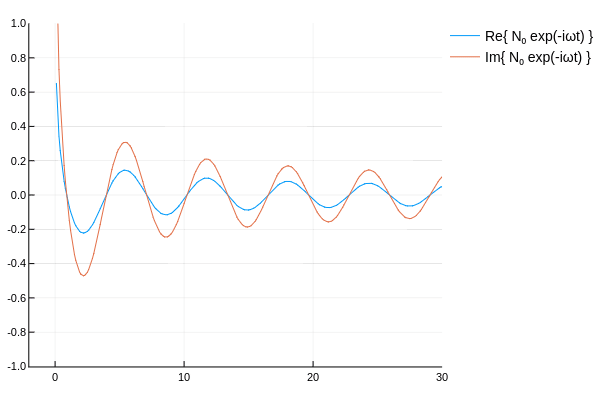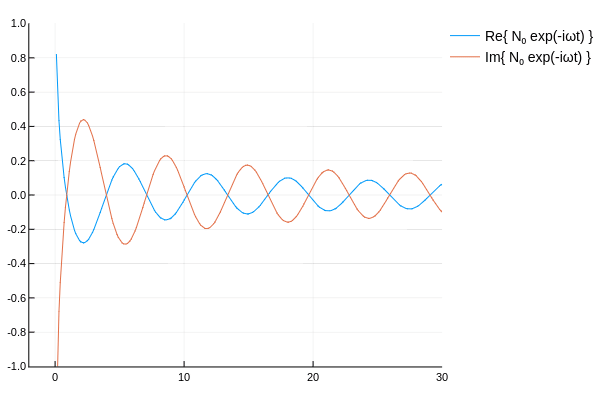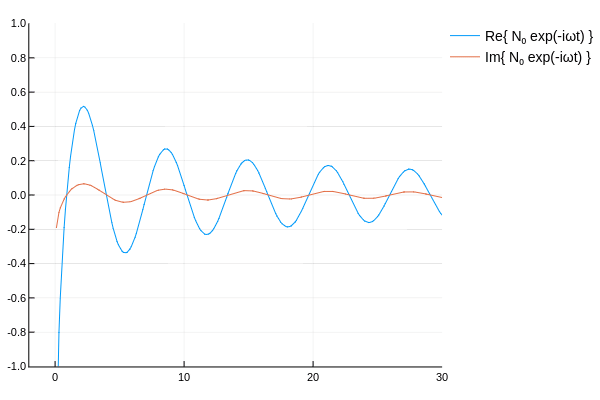
ハンケル関数の概形を確認するため,各種ベッセル関数に \(e^{-i\omega t}\) を乗じてアニメーションを作ってみた.
\( H_\nu^{(1)},\,H_\nu^{(2)} \) は互いに逆方向に伝播していく波を表していると確認できる.
その他 †
なんとなく,ベッセル関数に \(e^{-i\omega t}\) を乗じ,\(t\)を変動させ実部と虚部を表示して遊んでみた.